一、归因论证的本质与分类
定义:针对已发生的结果事实分析其根本原因(如“感冒是因穿得少”)。
核心特征:
- 结果必须既成事实(如“已感冒”),而非单纯陈述因果关系(如“着凉会导致感冒”)。
- 与因果关系的区别:
- 因果关系:描述“A可能导致B”(普遍规律)。
- 归因论证:锁定已发生事件的具体原因(个案分析)。
三大类型:
- 对比实验归因
- 特征:通过实验组(如久坐人群)与对照组(不久坐人群)的数据对比归因。
- 标志词:题干含“据调查显示”“实验表明”等。
- 时间对比归因
- 特征:纵向比较不同时间点的变化(如1990年vs现在的骨骼疾病率)。
- 原则:用变化解释变化(长期存在的因素不能作为变化原因)。
- 反常情况归因
- 特征:分析异常现象(如预期销量高但实际低迷)。
- 切入点:主客观维度(如“太贵买不起”属客观限制)。
二、归因论证的质疑与支持方法
质疑方法(力度从强到弱):
| 方法 | 操作 | 示例 |
|---|---|---|
| 否定此因 | 直接反驳原因合理性 | “穿得少不是感冒主因”(需提供依据) |
| 因果倒置 | 颠倒原因与结果 | “健康恶化导致走路减少”(非走路导致恶化) |
| 另有他因 | 提出其他原因(需分组正确) | “感冒是因病毒而非着凉” |
| 继发关联 | 揭示A、B均为C导致的结果(特殊他因) | “战争同时导致死亡和骨折” |
支持方法:
- 排除他因:控制其他变量,确保唯一归因(类比化学控制变量法)。
- 四圈支持法:构建完整对照实验(实验组与对照组仅目标变量不同)。
三、高频题型解题策略
- 直接根本原因题型
- 结构:两个竞争原因(原观点A vs 反对者B)导致同一结果。
- 解题口诀:
- 削弱反对者 → 构建“原观点A→反对者B→结果”链条。
- 支持反对者 → 构建“反对者B→原观点A→结果”链条。
- 补充对比实验设计场景方法目的缺对照组补充横向对比(如多地区)质疑(三圈法)仅时间纵向对比补充横向+时间维度支持(四圈法)
- 案例:
- 蚊子数量与温度关系:需同城多年数据(纵向),跨城对比无效。
- 城市创卫政策:需相似城市横向对比(政策效果不可逆)。
- 案例:
- 实验结果违背常识
- 步骤:
- 确认统计异常(如“抽烟喝酒者更长寿”)。
- 追溯实验漏洞(样本偏差、未控变量)。
- 关键:识别“不抽烟不喝酒群体可能存在健康隐患”等隐藏干扰。
- 步骤:
四、选项分析与避坑指南
- 错误选项特征:
- 非原因类(如讨论实验瑕疵但未涉及归因)。
- 伪他因(未验证实验组/对照组差异)。
- 模糊表述(“有些”“可能”)。
- 正确选项铁律:
- 必须包含原因分析(如“因样本特殊导致结论偏差”)。
- 力度排序:否定此因/因果倒置 > 另有他因 > 实验瑕疵。
五、数量论证的四大核心模型
本质:将数学关系融入逻辑论证的综合题型,需同时验证数据合理性与逻辑严谨性。
| 模型 | 典型陷阱 | 破解方法 | 案例 |
|---|---|---|---|
| 比例论证 | 仅用分子推断整体 | 补充分母数据对比 | 78%中耳炎患者来自二手烟家庭→需对比全体儿童二手烟家庭占比 |
| 抽样论证 | 样本特殊导致结论失真 | 验证样本代表性 | 春运列车上调查“购票难度”(样本均为已购票者) |
| 盐水模型 | 混淆部分与整体浓度关系 | 牢记“整体浓度介于两部分之间” | 10%与60%溶液混合≠70% |
| 容斥原理 | 忽略集合重叠 | 若A%+B%>100%,必有交集 | 80%员工会编程+70%会英语→必有人两者皆会 |
高频题型解题要点:
- 分数比较(如脱发率上升):
- 同时分析分子(脱发人数)、分母(总人数)变化。
- 口诀:分子分母要齐全,单看分子太片面!
- 人数 vs 人次:
- 人次=人数×频次(如11万张健身卡可能由3.5万人各办3张)。
- 乘积关系(如销量×价格):
- 警惕反向变化(单价↓可能被销量↑抵消)。
六、严谨逻辑关系的识别与解题策略
识别标志:题干含逻辑关联词(所有都/如果那么/除非否则)。
1. 质疑方法
- 核心方法:构造反例(a且非b)质疑a→b。示例:
题干:如果努力,那么成功(努力→成功)
质疑:有人努力但未成功(努力∧¬成功) - 特殊情况:用a→非b替代质疑(如航运公司案例)。
2. 支持方法
| 方法 | 操作 | 适用场景 |
|---|---|---|
| 搭桥法 | 补全论证断裂环节(如A→B的缺失链) | 论据与结论存在概念跳跃 |
| 三段论 | 满足“三概念各出现两次” | 含“所有”“有些”的推理 |
三段论规则:
- 结构:大前提(所有A是B) + 小前提(C是A) → 结论(C是B)
- 错误陷阱:
- 逆了:将A→B误作B→A
- 否了:从¬A推出¬B
- 分割谬误:将群体属性强加个体(如“四海学生来自五湖四海→小王是四海学生→故小王来自五湖四海”)
七、一般质疑方法的分类应用
1. 无论据结论:直接反驳结论(用A与非A的矛盾关系)。
原结论:购买医疗保险者会放任不良行为
质疑:疾病对健康的损害远非报销能弥补
2. 有论据结论:
| 类型 | 方法 | 案例 |
|---|---|---|
| 论据为主观观点 | 质疑论据可靠性 | “我认为黑猫不祥”→可质疑个人观点偏见 |
| 论据与结论无关 | 断点拆桥 | “第一场雪早→冬天冷”:降雪与气温无必然联系 |
| 结论含无中生有信息 | 针对新增内容批驳 | 论据“咖啡杯耐热”→结论“材料环保” |
3. 增加反向论据:
- 结构:虽然[论据],但是[反向证据],所以不[结论]。
示例:虽然咖啡在W国受欢迎(论据),但是价格过高(反向证据),所以实际消费低(质疑销量预期)。
八、实战避坑指南
1. 选项筛选原则:
- 数量题:
- 正确选项必含比例/分母数据(如“全体儿童中熬夜比例”)。
- 错误选项常犯“绝对数陷阱”(如“1000人胜场>800人”忽略总场次)。
- 逻辑题:
- “有些/个例”可能是正确答案(可构造反例)。
- 排除“维他因”(第三方原因未验证)。
2. 力度排序:
- 数量论证:比例完备 > 抽样修正 > 盐水定性
- 逻辑质疑:a且非b > a→非b > 主观质疑
九、翻译推理五大题型解题体系
核心逻辑:五大题型构成完整推理链,前一类是后一类的基础。
| 题型 | 特征 | 解题公式/方法 | 示例 |
|---|---|---|---|
| 等价推出 | 用命题推命题 | 逆否等价:¬B→¬A(与A→B等价) | 题干:下雨→地湿 → 等价选项:¬地湿→¬下雨 |
| 正推 | 已知事实+推理链 | 顺向推导(若A真,则B、C必真) | 已知A→B→C,且A发生 → C必然发生 |
| 逆推 | 目标结果为终点 | 反向递推(要D成立,需C→B→A成立) | 目标:D成立 → 需确保C→D且B→C且A→B |
| 两难推理 | “无论A与否,都B”结构 | 公式:A→B 且 ¬A→B ⇒ B必然发生 | 下雨去室内,不下雨去室外 → 今天必出门 |
| 范畴推理 | 含“所有”“有些”的集合关系 | 1. 画二分图(B/¬B)<br>2. 规则:<br> – 所有→特例→有些<br> – “有些是”推不出“有些不是” | 所有猫是动物→这只猫是动物→有些猫是动物 |
避坑指南:
- 逆否规则:仅能右侧推出,不可反向(A→B ≠ B→A)。
- 两难条件:所有推出关系必须已知为真。
- 范畴误区:
- “有些A是B”可推出“有些B是A”
- “有些A是B”不能推出“有些A不是B”
十、分析推理的两大核心方法
1. 真假分析三法(基础题型必保100%正确率)
| 方法 | 操作 | 适用场景 |
|---|---|---|
| 矛盾法 | 定位矛盾命题(一真一假) | 题干含“或/且”“所有/有些”矛盾 |
| 假设法 | 假设某命题真,验证是否矛盾 | 无矛盾时使用 |
| 代入法 | 将选项代入题干验证 | 复杂或耗时题型 |
矛盾关系总结:
- A∨B 矛盾 ¬A∧¬B
- A→B 矛盾 A∧¬B
- “所有A是B”矛盾“有些A不是B”
2. 日常分析四原则
两大切入点:
最大信息量(高频出现元素)
确定性信息(如“乙不是冠军”)
两大思维:
等价思维(转化表述):
“选123中几种” ⇨ “不选45”
“甲乙学历不同” ⇨ “甲≠乙学历”
极限思维(极端值验证)
四大模型:
| 模型 | 功能 | 案例 |
|---|---|---|
| 冠军模型 | 利用唯一性锁定答案 | 四人猜冠军,仅一人正确 → 找出现频次最低的选项 |
| 容斥模型 | 计算集合重叠 | 80%会编程+70%会英语 → 至少50%两者都会 |
| 多重身份 | 处理角色交叉 | 一人兼销售/财务两职 |
| 数独模型 | 解决唯一对应关系 | 五人五种颜色一一匹配 |
十一、推理方式与论证结构辨析
1. 三大推理类型:
| 类型 | 特征 | 可靠性 |
|---|---|---|
| 演绎推理 | 公式化(如三段论) | 绝对有效(若前提真) |
| 归纳推理 | 部分→整体 | 不完全归纳:或然性 |
| 类比推理 | 特殊→特殊 | 支持力度最弱 |
2. 演绎推理典型设错:
- 逆了:A→B 误作 B→A
- 否了:A→B 误作 ¬A→¬B
- 分割谬误:群体属性强加个体错误案例:四海学生来自五湖四海 → 小王是四海学生 → 故小王来自五湖四海
3. 论证结构漏洞:
- 不完全归纳:样本偏差导致结论失真(如“我见的乌鸦都黑→天下乌鸦一般黑”)。
- 类比推理:忽略本质差异(如“鸟会飞→鸵鸟是鸟故鸵鸟会飞”)。
十二、实战技巧精选
1. 冠军模型速解:
- 步骤:
- 翻译所有条件(如“冠军是A或B”)
- 统计元素出现频次
- 锁定唯一出现项为真
示例:四人猜测中,仅一人说“冠军是C” → 若C在其他描述中未出现,则此人正确。
2. 三段论验证法:
- 规则:
- 三概念各出现两次
- 前提无否定 → 结论无否定
- 前提含“有些” → 结论含“有些”
十三、命题逻辑核心框架
1. 复合命题三大类型
| 类型 | 形式 | 真假规则 | 矛盾关系 | 特性 |
|---|---|---|---|---|
| 联言命题 | p∧q(p且q) | 全真为真,一假则假 | ¬p∨¬q | 必须同时成立 |
| 相容选言 | p∨q(p或q) | 一真则真,全假才假 | ¬p∧¬q | 否一推一(¬p→q) |
| 不相容选言 | 要么p要么q | 一真一假为真 | (p∧q)∨(¬p∧¬q) | 不可同真同假 |
2. 假言命题深度解析
翻译规则:

真假判断:
唯一假情况:p真且q假(p∧¬q)
真值表:
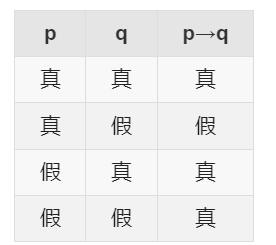
必要/充分标志词:
必要条件(后件):基础、关键、前提、必须、不可或缺
充分条件(前件):如果…那么、只要…就
十四、直言命题与模态命题系统
1. 直言命题六形式
| 类型 | 示例 | 矛盾 | 推出关系 |
|---|---|---|---|
| 全称肯定 | 所有S是P | 有些S不是P | → 某个S是P → 有些S是P |
| 全称否定 | 所有S不是P | 有些S是P | → 某个S不是P → 有些S不是P |
| 特称肯定 | 有些S是P | 所有S不是P | 可推出有些P是S |
反对关系:
- 上反对(所有是 vs 所有不是):必有一假(可同假)
- 下反对(有些是 vs 有些不是):必有一真(可同真)
2. 模态命题矛盾转换
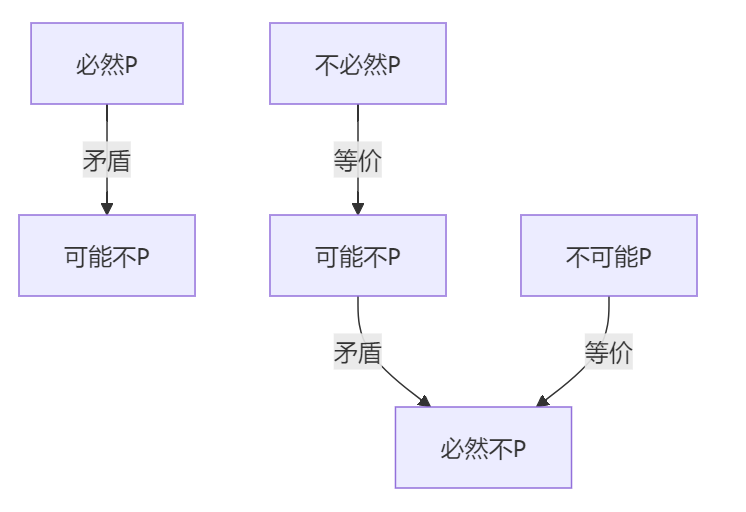
十五、归因论证全体系总结
1. 三大归因类型对比
| 类型 | 标志特征 | 质疑方法 | 支持方法 |
|---|---|---|---|
| 对比实验归因 | 实验组vs对照组 | 因果倒置 > 否定此因 > 另有他因 | 排除他因 |
| 时间对比归因 | “1990年vs现在”变化 | 指出非同步变化因素 | 锁定唯一变量 |
| 反常情况归因 | 预期与结果矛盾 | 增加反向论据(主客观维度) | 解释反常机制 |
2. 实验设计黄金法则
横向对比(一次性事件):政策类(如创卫):需相似城市对比
纵向对比(连续变量):温度与蚊子数量:需同城多年数据
四圈支持法:
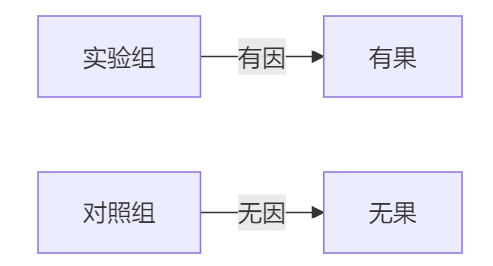
3. 选项筛选铁律
- 归因类:必须含原因分析(排除“维他因”选项)
- 力度排序:
否定此因 ≈ 因果倒置 > 另有他因 > 实验瑕疵 - 反常处理:
- 确认统计悖论(如“抽烟者长寿”)
- 追溯隐藏变量(如“不抽烟群体有健康隐患”)
十六、逻辑推理方式辨析
1. 三大推理类型特征
| 类型 | 结构 | 可靠性 | 典型错误 |
|---|---|---|---|
| 演绎推理 | 公式推导(三段论) | 绝对有效 | 逆了(A→B 误作 B→A) |
| 归纳推理 | 部分→整体 | 不完全归纳或然 | 样本偏差(“乌鸦全黑”) |
| 类比推理 | 特殊A→特殊B | 支持力度最弱 | 忽略本质差异(鸟→鸵鸟) |
2. 分割谬误专项
本质:将群体属性错误赋予个体
案例拆解:
大前提:四海学生来自五湖四海(群体属性)
小前提:小王是四海学生(个体)
错误结论:小王来自五湖四海(个体被赋予群体属性)