资料分析中,高效准确的速算能力是得分关键。本文系统梳理加法、减法、乘法的核心速算技巧,结合真题案例解析,助你快速提升计算效率。
一、加法技巧
1. 尾数法
适用场景:整数精确求和(如“高校数量323所”),不适用含四舍五入的数据(如“234.3万人”)。
操作步骤:
- 选项末位不同 → 计算最后一位(例:5+2=7 )。
- 选项末两位不同 → 计算最后两位(例:92+111=203 )。
避坑提示:警惕时间段审题错误(如将2014-2019误作2014-2017)。
2. 高位叠加法
核心优势:
- 省去抄写时间(5个数省20秒);
- 减少进位运算;
- 可灵活终止计算(按选项精度需求)。
操作步骤:
- 从高位向低位逐级相加(千位→百位→十位→个位);
- 阶梯式书写结果(如千位结果写最左,百位右移一格)。
案例演示:
题目:计算2016-2020年销售额(单位:亿元):3156, 3479, 3641, 4093, 4030
速算:
- 千位:3+3+3 + 4 + 4 = 17
- 百位:(1+4+6+0+0) + (5+7+4+9+3) = 11 + 28 = 39 → 进位3,余9
- 结果:17,000 + 3,900 = 20,900(精确值20,899)
二、减法技巧
1. 整数基准值法
核心思想:将复杂减法(需借位)拆分为两个简单减法。
操作步骤:
- 选取整百/整千基准值(如600);
- 拆解:被减数 – 基准值 + 基准值 – 减数。
案例:632 – 589 = (632 – 600) + (600 – 589) = 32 + 11 = 43
2. 21分段法与12分段法
选择依据:
- 个位够减 → 用21分段(前两位一组,末位单独算):例:396 – 273 → 39|6 – 27|3 = 12|3 = 123
- 个位不够减 → 用12分段(首位单独算,后两位一组):例:264 – 192 → 2|64 – 1|92 = 1|(-28) = 100 – 28 = 72
真题应用:
题目:2021年7-9月光纤用户增量(单位:万户):7月484→479,8月489→484,9月496→489。问增量超500万户的月份数。
速算:
- 7月:484-479 → 百位差=0,十位84-79=5(需借位)→ 不足500
- 8月:489-484 → 百位差=0,十位89-84=5(无借位)→ 超500
- 9月:496-489=7 → 直接超500
三、乘法技巧
1. 小分互换法
核心思想:将百分数转为分数简化运算(增长率<20%时最优)。
常用转换表:
| 百分数 | 分数 | 计算等价 |
|---|---|---|
| 25% | 1/4 | ÷4 |
| 12.5% | 1/8 | ÷8 |
| 20% | 1/5 | ÷5 |
案例:
- 784 × 25% → 784 ÷ 4 = 196
- 632 × 12.5% → 632 ÷ 8 = 79
2. 拆分法(包子理论)
核心思想:将1%定义为“1个包子”,组合计算。
操作步骤:
- 拆分复杂百分数(如45% = 50% – 5%);
- 计算基础单位:
- 50% = 原数 ÷ 2
- 10% = 原数 ÷ 10
- 1% = 原数 × 0.01
真题应用:
题目:母婴消费总额34600亿元,占比最高品类达26%,求其金额。
速算:
- 25% = 34600 ÷ 4 = 8650
- 1% = 346
- 26% ≈ 8650 + 346 = 8996
关键技巧对比表
| 技巧 | 适用场景 | 优势 |
|---|---|---|
| 尾数法 | 整数精确求和 | 避免全量计算 |
| 高位叠加 | 多位数加法 | 减少进位,灵活终止 |
| 基准值法 | 需借位的减法 | 拆解复杂运算 |
| 小分互换 | 乘数≤20%的乘法 | 转化除法提速 |
四、除法技巧
1. 拆分法
优化本质:对直除运算的改进,特别适合比重计算(如基期量、增量)。
三大拆分策略:
- 50%原则:当分子≈分母50%时,先拆50%计算.剩余部分按”包子法”估算(将分母1%视为一个包子价格)。示例说明:196-618可拆为309/608(50%)减去13/618(约2%),结果约为48%
- 100%原则:分子≈分母时,先拆100%. 比如888/912=1-24/912
- 小比例拆分:根据情况拆出10%、5%或1%作为计算单位.
方法对比:
| 方法 | 适用场景 | 优势 |
|---|---|---|
| 拆分法 | 分子≤分母 | 避免多步试商 |
| 直除法 | 高精度要求 | 需多次试商 |
五、ABRX关系模型
1. 现期(B)与基期(A)定义
- 基期(A):比较基准时期(口诀:“与谁比,谁为基期”)。
- 现期(B):当前时期(B=”本期”拼音首字母,A为B前一字母)。
示例:2019年社会消费品总额38094亿元(B),较2018年(A)增长8.0%。
2. 增长量(X)与增长率(R)
- 增长量(X):绝对差值(X=B−A),可正可负(如体重190→180,X=-10)。
- 增长率(R):相对变化率(R=X/A),等价增速/增幅。
3. 四大核心公式
| 已知条件 | 公式 | 案例验证 |
|---|---|---|
| A和B | X=B−A,R=X/A | A=8000,B=10000 → X=2000,R=25% |
| A和R | X=A×R,B=A+X | A=8000,R=10% → X=800,B=8800 |
| B和R | A=B/(1+R),X=B−A | B=10000,R=25% → A=8000,X=2000 |
| X和R | A=X/R,B=A+X | X=2000,R=25% → A=8000,B=10000 |
真题应用:
题目:2016年H市高新技术产品出口424.23亿元,增长7.6%,求2015年出口额。
计算:A=424.23/1+7.6%≈394.3 → 394.3亿元
六、四幺五份数法
1. 核心原理
份数关系:将增长率R转化为最简分数n/m,则:
- 基期(A) = m份
- 增长量(X) = n份
- 现期(B) = m + n份
示例:R=25%=41 → A:X:B = 4:1:5
2. 操作步骤
分数转换:
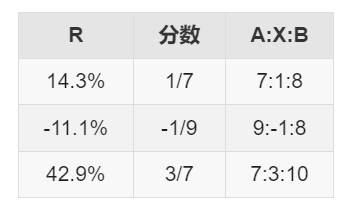
求单份量:单份量=B/总份数
解目标量:
X=单份量 *n
A=B−X(优先用减法避免误差)
3. 误差控制与真题
核心规则:
- R与标准分数偏差>2%时慎用(如23%用1/4误差大);
- 负增长:份数带负号(例:R=-25% → A:X:B=4:-1:3)。
真题演练:
题目:现期量328,增长率≈49.8%(按50%估算),求增量X。
速算:
- R≈50%=1221 → A:X:B=2:1:3
- 单份量=328÷3≈109.3
- X≈109.3 → 最接近109
题目:现期量694,增长率≈-33.3%,求基期A。
速算:
- R≈-33.3%=−13−31 → A:X:B=3:-1:2
- 单份量=694÷2=347
- A=3×347=1041
七、假设分配法
1. 核心思想与适用条件
核心公式:B=A+X(现期=基期+增量),X=A×R
黄金场景:
- 增长率 R ≤ 10%(或接近10%)
- 基期值 A 接近整数(如整百/整千)
禁忌:负增长率(计算繁琐,建议换方法)
2. 三步操作流程
| 步骤 | 操作说明 | 案例演示(B=662,R=8%) |
|---|---|---|
| 1. 定基数 | 选接近 B 的整百/整千数 | 取基数600 |
| 2. 初分配 | 计算 基数×R | X1=600×8%=48 |
| 3. 微调 | 剩余值按比例估算 | 剩余(62-48)14:按8%近似值10%分配≈1.4,向下取整为1 → X=49,A=613 |
取整规则:
- R > 10% → 向上取整(如12%按10%基准上浮)
- R < 10% → 向下取整(如8%按10%基准下调)
- 根据增长率就近取整(8%参照10%,6%参照5%,3%参照5%)
八、应用案例精解
案例:城市供水管道增长长度(国考真题)
题干:2021年供水管道105.99万公里,增长5.26%,求增量。
假设分配法:
- 基数取100:X1=100×5.26%=5.26
- 剩余5.99:按5%分配≈0.3 → X≈5.56
方法总结与选择指南
| 场景 | 首选方法 | 替代方案 |
|---|---|---|
| 求增量(R<10%) | 假设分配法 | 四幺五法 |
| 求基期(R=1/3,1/4等分数) | 四幺五法 | 拆分法 |
| 选项差距极小(<1%) | 公式 X=B×R/(1+R) | 直除法 |
| 多基期比较(如差值/平均值) | 假设分配法 | 高位叠加法 |